نصف یک دوم چقدر است ریاضی ششم

پاسخ این سوال که نصف یک دوم چقدر است ریاضی ششم، به طور خلاصه «یک چهارم» یا همان 1/4 است. این مفهوم از مباحث اساسی کسرها در پایه ششم ابتدایی به شمار می رود که درک آن برای دانش آموزان از اهمیت بالایی برخوردار است. در ادامه به بررسی جامع و روش های مختلف محاسبه این مسئله می پردازیم.

در دنیای ریاضیات پایه، به ویژه در مقطع ششم ابتدایی، درک مفاهیم بنیادی کسرها نقش محوری در پیشرفت تحصیلی دانش آموزان دارد. کسرها نه تنها ابزاری برای نمایش بخش هایی از یک کل هستند، بلکه در محاسبات روزمره و درک مباحث پیچیده تر ریاضی نیز کاربرد فراوان دارند. یکی از چالش های رایج برای دانش آموزان و حتی گاهی والدین، درک و محاسبه عباراتی مانند نصف یک دوم است. این عبارت، با وجود سادگی ظاهری، نیازمند فهم عمیق از عملیات کسرها و ارتباط آن ها با مفهوم تقسیم و ضرب است. هدف از این مقاله، ارائه توضیحی کامل، شفاف و گام به گام برای محاسبه این عبارت با تمرکز بر مفاهیم ریاضی پایه ششم ابتدایی است تا دانش آموزان، والدین و معلمان بتوانند به راحتی مفهوم نصف کردن کسرها را درک کرده و روش های مختلف حل آن را بیاموزند.

مفهوم نصف در ریاضیات

مفهوم نصف یکی از ابتدایی ترین و پرکاربردترین مفاهیم در ریاضیات و زندگی روزمره ماست. وقتی از نصف چیزی صحبت می کنیم، منظورمان تقسیم آن شیء یا مقدار به دو قسمت مساوی است. از منظر ریاضی، نصف کردن یک عدد یا یک کسر می تواند به دو شیوه اصلی بیان شود:

1. تقسیم بر عدد 2: هرگاه بخواهیم نصف یک مقدار را محاسبه کنیم، می توانیم آن مقدار را بر 2 تقسیم کنیم. به عنوان مثال، نصف عدد 6 می شود 6 ÷ 2 = 3.
2. ضرب در کسر 1/2: روش دیگر برای محاسبه نصف یک مقدار، ضرب آن مقدار در کسر 1/2 است. کسر 1/2 دقیقاً نشان دهنده نصف یک واحد کامل است. مثلاً، نصف عدد 10 می شود 10 × 1/2 = 5.

این دو رویکرد (تقسیم بر 2 و ضرب در 1/2) در نهایت به یک نتیجه منجر می شوند، زیرا تقسیم بر یک عدد معادل ضرب در معکوس آن عدد است. در مورد عدد 2، معکوس آن 1/2 است. درک این هم ارزی برای کار با کسرها ضروری است. برای دانش آموزان پایه ششم، تسلط بر این مفهوم پایه ای، پلی برای ورود به دنیای عملیات پیشرفته تر روی کسرها، از جمله ضرب و تقسیم آن ها، فراهم می کند. این مفهوم نه تنها در مباحث نظری، بلکه در مسائل کاربردی روزمره، مانند تقسیم مواد غذایی، پول، یا زمان، اهمیت بسزایی دارد.

کسر یک دوم (1/2) به زبان ساده

کسر یک دوم که به صورت 1/2 نمایش داده می شود، یکی از ساده ترین و بنیادی ترین کسرهاست و مفهوم آن به معنای نیمی از یک واحد کامل است. در این کسر، عدد 1 که در بالای خط کسر قرار دارد، صورت کسر نامیده می شود و تعداد قسمت هایی را که انتخاب کرده ایم یا مورد نظر ماست، نشان می دهد. عدد 2 که در پایین خط کسر قرار دارد، مخرج کسر نامیده می شود و نشان دهنده تعداد کل قسمت های مساوی است که واحد کامل به آن ها تقسیم شده است.

برای درک بهتر، می توانیم تصور کنیم یک شیء واحد مانند یک سیب، یک پیتزا یا یک کیک را به دو قسمت کاملاً مساوی تقسیم کرده ایم. هر یک از این قسمت های مساوی، همان یک دوم یا 1/2 کل شیء محسوب می شود. از نظر بصری، اگر یک دایره را به دو نیمه مساوی تقسیم کنیم، و یکی از این نیمه ها را رنگ کنیم، قسمت رنگ شده نشان دهنده 1/2 آن دایره است. این کسر معادل اعشاری 0.5 نیز هست؛ یعنی اگر یک واحد را بر 2 تقسیم کنیم، حاصل 0.5 خواهد بود. این ارتباط بین کسر و عدد اعشاری نیز در ریاضیات ششم ابتدایی مورد بررسی قرار می گیرد و به دانش آموزان کمک می کند تا درک جامع تری از اعداد داشته باشند.

روش اول: استفاده از تقسیم کسرها

یکی از راه های محاسبه نصف یک دوم، استفاده از عملیات تقسیم کسرهاست. وقتی می گوییم نصف یک دوم، در واقع منظورمان این است که کسر یک دوم را بر 2 تقسیم کنیم. این مسئله به صورت ریاضی به شکل زیر بیان می شود:


1/2 ÷ 2


برای حل این تقسیم، مراحل زیر را دنبال می کنیم:

1. تبدیل عدد صحیح به کسر: ابتدا باید عدد صحیح 2 را به یک کسر تبدیل کنیم. هر عدد صحیحی را می توان با قرار دادن مخرج 1 به کسر تبدیل کرد. بنابراین، عدد 2 به صورت 2/1 نوشته می شود.

   
1/2 ÷ 2/1


2. تغییر عمل تقسیم به ضرب: قانون تقسیم کسرها بیان می کند که برای تقسیم یک کسر بر کسر دیگر، کسر اول را ثابت نگه می داریم و آن را در معکوس کسر دوم (مقسوم علیه) ضرب می کنیم. معکوس کسر 2/1، کسر 1/2 است (یعنی صورت و مخرج را جابجا می کنیم).

   
1/2 × 1/2


3. محاسبه نهایی ضرب کسرها: اکنون که عملیات به ضرب کسرها تبدیل شده است، صورت ها را در هم ضرب می کنیم و مخرج ها را نیز در هم ضرب می کنیم.
   • صورت × صورت: 1 × 1 = 1
   • مخرج × مخرج: 2 × 2 = 4

   بنابراین، حاصل ضرب برابر است با 1/4.

مثال حل شده با جزئیات کامل:

فرض کنید می خواهیم نصف کسر 3/4 را پیدا کنیم. این یعنی 3/4 ÷ 2.

1. تبدیل 2 به کسر: 2/1
2. تغییر تقسیم به ضرب و معکوس کردن کسر دوم: 3/4 × 1/2
3. ضرب صورت ها در هم: 3 × 1 = 3
4. ضرب مخرج ها در هم: 4 × 2 = 8
5. نتیجه نهایی: 3/8

در نتیجه، نصف کسر 1/2 برابر با 1/4 است. این روش به دانش آموزان کمک می کند تا با اصول تقسیم کسرها به خوبی آشنا شوند و آن را در حل مسائل مختلف به کار ببرند.

روش دوم: استفاده از ضرب کسرها (روش مستقیم و پرکاربرد)

معمولاً در ریاضیات، زمانی که از عبارت نصفِ یا درصدِ چیزی صحبت می شود، منظور انجام عمل ضرب است. به عنوان مثال، نصفِ 6 یعنی 1/2 × 6. بر همین اساس، برای محاسبه نصفِ یک دوم، می توانیم این مفهوم را به عنوان یک دوم ضربدر یک دوم تفسیر کنیم. این روش از سادگی و کارایی بالایی برخوردار است و در بسیاری از موارد به عنوان روش اصلی برای حل این گونه مسائل به کار می رود.

مسئله به صورت ریاضی به شکل زیر بیان می شود:


1/2 × 1/2


برای حل این ضرب کسرها، مراحل زیر را دنبال می کنیم:

1. ضرب صورت ها در هم: صورت کسر اول (1) را در صورت کسر دوم (1) ضرب می کنیم.

   
1 × 1 = 1


2. ضرب مخرج ها در هم: مخرج کسر اول (2) را در مخرج کسر دوم (2) ضرب می کنیم.

   
2 × 2 = 4


بنابراین، حاصل ضرب برابر است با 1/4.

این روش به دلیل سادگی و کم بودن مراحل، اغلب برای دانش آموزان جذاب تر و قابل فهم تر است. مفهوم نصفِ به صورت مستقیم به عمل ضرب در 1/2 ترجمه می شود و پیچیدگی های تبدیل تقسیم به ضرب را ندارد. با این حال، درک هر دو روش (تقسیم و ضرب) به تقویت بنیادهای ریاضی و توانایی انتخاب بهترین روش برای حل مسائل مختلف کمک می کند.

مثال حل شده با جزئیات کامل:

فرض کنید می خواهیم نصف کسر 5/8 را پیدا کنیم.

1. ترجمه نصفِ به ضرب در 1/2: 5/8 × 1/2
2. ضرب صورت ها در هم: 5 × 1 = 5
3. ضرب مخرج ها در هم: 8 × 2 = 16
4. نتیجه نهایی: 5/16

همانطور که مشاهده می شود، در هر دو روش (تقسیم بر 2 و ضرب در 1/2)، به پاسخ یکسان 1/4 می رسیم. این نشان دهنده اعتبار و صحت هر دو روش است و دانش آموزان می توانند با اطمینان از هر یک از این روش ها برای حل مسائل مشابه استفاده کنند.

تاریخچه مختصر مفهوم کسر و نصف

مفهوم کسر و درک بخش هایی از یک کل، ریشه های بسیار کهنی در تاریخ ریاضیات دارد. تمدن های باستانی، به ویژه مصریان و بابلیان، از اولین اقوامی بودند که با کسرها سروکار داشتند. مصریان باستان، که حدود 4000 سال پیش می زیستند، از کسرهای واحد (کسرهایی که صورت آن ها 1 بود، مانند 1/2، 1/3، 1/4) به شکل گسترده ای استفاده می کردند. پاپیروس های ریاضیاتی مانند پاپیروس ریند که از مهم ترین منابع دانش ریاضیات مصر باستان است، مملو از مسائل و محاسبات کسری است که نشان دهنده نیاز آن ها به تقسیم مقادیر در زندگی روزمره، از جمله تقسیم زمین، غذا یا غلات بود.

مفهوم نصف به عنوان یکی از بنیادی ترین بخش بندی ها، طبیعتاً از همان ابتدا مورد توجه بوده است. تقسیم یک واحد به دو قسمت مساوی، اساسی ترین شکل تقسیم و کسربندی است. این مفهوم نه تنها در ریاضیات، بلکه در جنبه های فرهنگی و حتی دینی بسیاری از تمدن ها نیز حضور داشته است. به عنوان مثال، در تقسیم میراث یا منابع، نصف کردن یکی از رایج ترین روش ها برای عدالت و برابری بوده است.

با گذشت زمان و پیشرفت تمدن ها، ریاضیدانان یونانی، هندی، عرب و نهایتاً اروپایی، سیستم کسور را توسعه داده و آن را به شکل امروزی (با صورت و مخرج) استاندارد کردند. اعراب نقش مهمی در انتقال و توسعه سیستم کسری هندی به اروپا داشتند و مفاهیمی مانند جمع، تفریق، ضرب و تقسیم کسرها به تدریج فرمول بندی و تدریس شدند. در این مسیر تکاملی، درک عمیق تر از عملیات روی کسرها، مانند نصف کردن یک کسر، از مسائل پایه و مهمی بود که به تدریج در سرفصل های آموزشی قرار گرفت.

امروزه، آنچه دانش آموزان کلاس ششم درباره کسرها می آموزند، نتیجه هزاران سال تلاش و توسعه فکری است. درک این ریشه های تاریخی می تواند به دانش آموزان کمک کند تا اهمیت این مفاهیم را فراتر از صرفاً یک مسئله درسی درک کنند و ببینند که چگونه این ایده های بنیادین، زندگی و دانش بشر را در طول تاریخ شکل داده اند.

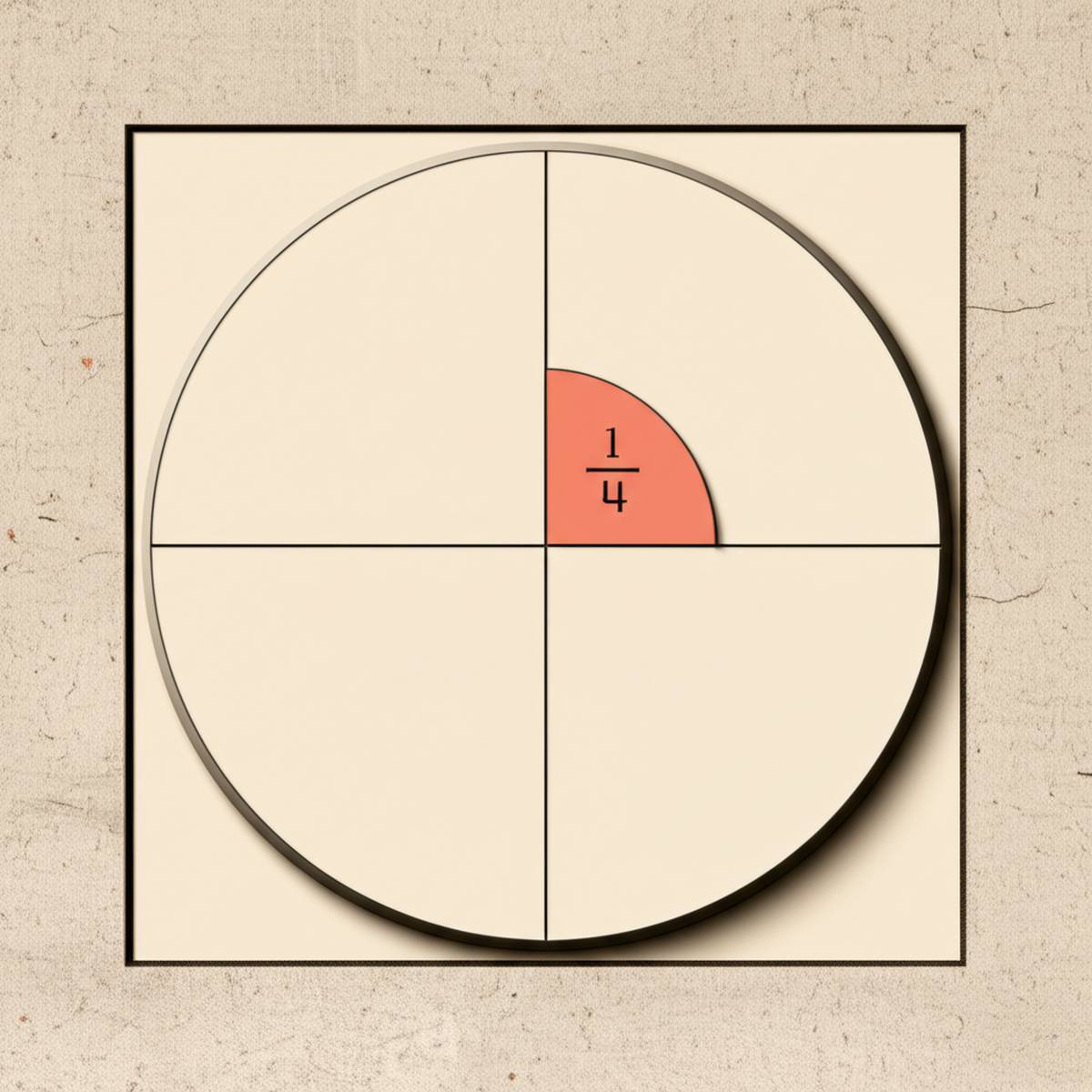
درک بصری: با استفاده از شکل و نمودار

یکی از مؤثرترین راه ها برای درک مفاهیم ریاضی، به خصوص کسرها، استفاده از تصاویر و نمودارهای بصری است. این روش به دانش آموزان کمک می کند تا مفاهیم انتزاعی را به صورت ملموس تری مشاهده کنند و درک عمیق تری از آن ها پیدا کنند. برای درک نصف یک دوم، می توانیم از یک شکل ساده مانند یک دایره یا یک مستطیل استفاده کنیم:

1. گام اول: نمایش یک دوم (1/2)
   * یک دایره یا مستطیل کامل را در نظر بگیرید. این شکل، واحد کامل ماست.
   * این شکل را دقیقاً از وسط به دو قسمت مساوی تقسیم کنید (مثلاً با کشیدن یک خط در وسط).
   * یکی از این دو قسمت را رنگ کنید. قسمت رنگ شده نشان دهنده کسر 1/2 از کل شکل است.
2. گام دوم: نصف کردن یک دوم
   * حالا قسمت رنگ شده (همان 1/2) را در نظر بگیرید. ما می خواهیم نصف این قسمت را پیدا کنیم.
   * این قسمت رنگ شده را نیز به دو بخش کاملاً مساوی تقسیم کنید.
   * وقتی این کار را انجام می دهید، در واقع کل شکل اولیه به چهار قسمت مساوی تقسیم شده است.

نتیجه بصری:

با انجام این مراحل، متوجه می شوید که از چهار قسمت مساوی که کل شکل به آن تقسیم شده، تنها یک قسمت کوچک تر، همان نصفِ قسمت رنگ شده اولیه (نصفِ 1/2) را نشان می دهد. این قسمت کوچک تر که حالا رنگی شده، دقیقاً یک چهارم (1/4) کل شکل اصلی است.

تصویرسازی ذهنی یا ترسیم این مراحل، به وضوح نشان می دهد که نصف یک دوم برابر با یک چهارم کل است. این روش به ویژه برای دانش آموزانی که یادگیری بصری قوی تری دارند، بسیار مفید است و کمک می کند تا مفاهیم کسری را از حالت صرفاً عددی خارج کرده و به آن ها معنای عینی ببخشد.

برای مثال، تصور کنید یک پیتزای کامل دارید. اگر آن را به دو قسمت مساوی تقسیم کنید، هر قسمت 1/2 پیتزا است. حالا اگر یکی از این نیمه ها را (که 1/2 کل پیتزا بود) دوباره از وسط نصف کنید، به یک تکه کوچک تر می رسید. این تکه کوچک تر، در واقع 1/4 (یک چهارم) پیتزای اصلی شماست. این درک بصری، پایه محکمی برای انجام محاسبات کسری بدون نیاز به حفظ کردن فرمول ها فراهم می کند.

ارتباط با اعداد اعشاری: نصف ۰.۵ چقدر است؟

درک ارتباط بین کسرها و اعداد اعشاری، یکی از مهارت های مهم در ریاضیات ششم ابتدایی است. کسر 1/2 و عدد اعشاری 0.5 در واقع دو شیوه مختلف برای نمایش یک مقدار واحد هستند. به عبارت دیگر، 1/2 به معنای یک تقسیم بر دو است که حاصل آن در سیستم اعشاری 0.5 می شود.

بنابراین، وقتی سوال می شود نصف یک دوم چقدر است؟، می توانیم آن را معادل نصف 0.5 چقدر است؟ نیز در نظر بگیریم. برای محاسبه نصف 0.5 به صورت اعشاری، می توانیم از دو روش مشابه کسرها استفاده کنیم:

1. تقسیم 0.5 بر 2:

   
0.5 ÷ 2 = 0.25


   برای انجام این تقسیم، کافیست 5 دهم را بر 2 تقسیم کنید. 5 تقسیم بر 2 می شود 2.5. حال چون 5 دهم بود، پاسخ می شود 25 صدم یا 0.25.

2. ضرب 0.5 در 0.5:

   
0.5 × 0.5 = 0.25


   در این روش، ضرب اعداد اعشاری را انجام می دهیم. ابتدا اعداد را بدون در نظر گرفتن اعشار در هم ضرب می کنیم: 5 × 5 = 25. سپس تعداد ارقام اعشاری در دو عدد اولیه را می شماریم (در 0.5 یک رقم اعشار و در 0.5 دیگر نیز یک رقم اعشار، در مجموع دو رقم اعشار). بنابراین، در حاصل ضرب (25) نیز باید دو رقم اعشار از سمت راست جدا کنیم که منجر به 0.25 می شود.

هر دو روش به پاسخ یکسان 0.25 می رسند. اکنون، برای ارتباط مجدد با کسرها، باید بدانیم که 0.25 نیز معادل کسری 1/4 (یک چهارم) است. زیرا 0.25 را می توان به صورت 25/100 نوشت که با ساده سازی (تقسیم صورت و مخرج بر 25) به 1/4 تبدیل می شود. این ارتباط سه گانه (کسر 1/2، اعشار 0.5، و معادل نهایی کسر 1/4، اعشار 0.25) نشان دهنده هم خانواده بودن این مفاهیم است و درک آن به دانش آموزان کمک می کند تا انعطاف پذیری بیشتری در حل مسائل ریاضی داشته باشند و از ابزارهای مختلف برای رسیدن به پاسخ صحیح استفاده کنند.

اهمیت درک نصف یک دوم در ریاضیات پیشرفته تر

مفهوم به ظاهر ساده نصف یک دوم تنها یک تمرین مقدماتی در ریاضی ششم ابتدایی نیست، بلکه پایه ای اساسی برای درک مفاهیم پیچیده تر در مراحل بالاتر تحصیلی و حتی در کاربردهای علمی و مهندسی است. درک عمیق این مفهوم، دانش آموزان را برای موفقیت در مباحث آتی ریاضی آماده می سازد.

1. تقویت درک عملیات با کسرها: تسلط بر نصف یک دوم به دانش آموزان کمک می کند تا ضرب و تقسیم کسرها را به خوبی درک کنند. این مهارت، ستون فقرات جبر کسری و معادلات حاوی کسرهاست که در مقاطع بالاتر از اهمیت ویژه ای برخوردار است.
2. مقدمه ای بر توابع و نسبت ها: نصف کردن، در واقع یک نسبت ثابت (1:2) را نشان می دهد. این دیدگاه به دانش آموزان کمک می کند تا بعدها مفهوم نسبت، تناسب و حتی توابع خطی (مانند f(x) = 1/2x) را بهتر درک کنند.
3. درک احتمال: در مبحث احتمال، بسیاری از مسائل بر اساس تقسیم بندی و کسور بیان می شوند. مثلاً احتمال پرتاب یک سکه و آمدن رو 1/2 است. اگر بخواهیم احتمال دو اتفاق متوالی را حساب کنیم، نیاز به ضرب کسرها داریم (مثلاً احتمال دو بار رو آوردن متوالی 1/2 × 1/2 = 1/4).
4. کاربرد در هندسه و اندازه گیری: در هندسه، محاسبه نصف مساحت، نصف محیط یا نصف حجم، به طور مستقیم به این مفاهیم برمی گردد. نصف کردن یک بعد برای ایجاد یک شکل جدید یا محاسبه ویژگی های آن، کاربردهای فراوانی دارد.
5. مفاهیم پیشرفته تر (حد و انتگرال): حتی در ریاضیات عالی مانند حسابان، مفاهیم حد و انتگرال به نوعی با تقسیم بندی های بی نهایت کوچک (و نصف کردن های متوالی) مرتبط هستند که از همین درک بنیادین ریشه می گیرند.

به طور خلاصه، نصف یک دوم فراتر از یک مسئله درسی است؛ این یک سنگ بنا برای توسعه تفکر ریاضیاتی، حل مسئله و درک جهان اطراف به زبان اعداد و روابط است. تقویت این درک در پایه ششم، سرمایه گذاری مهمی برای آینده تحصیلی و حرفه ای دانش آموزان خواهد بود.

اشتباهات رایج و چگونه از آنها دوری کنیم

در حین یادگیری مفهوم نصف یک دوم و عملیات روی کسرها، دانش آموزان ممکن است دچار برخی اشتباهات رایج شوند. شناخت این اشتباهات و آگاهی از راهکارهای جلوگیری از آن ها، می تواند فرآیند یادگیری را تسهیل کند.

1. اشتباه گرفتن نصف یک دوم با نصف عدد 2:
   * اشتباه: برخی دانش آموزان ممکن است تصور کنند نصف یک دوم یعنی نصف عدد 2 که برابر با 1 است.
   * راهکار: تأکید بر کلمه یک دوم به عنوان یک مقدار (یک کسر) و نه یک عدد صحیح. یادآوری که 1/2 خودش نیمی از یک چیز است و ما می خواهیم نصف همان نیمه را پیدا کنیم.
2. فقط نصف کردن مخرج:
   * اشتباه: ممکن است دانش آموز فقط مخرج کسر را نصف کند و کسر 1/1 را به اشتباه به عنوان پاسخ در نظر بگیرد.
   * راهکار: توضیح دهید که نصف کردن یک کسر به معنای ضرب آن در 1/2 (یا تقسیم بر 2) است و این عملیات شامل هر دو بخش صورت و مخرج (در نهایت) می شود. استفاده از روش ضرب صورت در صورت و مخرج در مخرج می تواند این اشتباه را برطرف کند.
3. عدم درک مفهوم از در کسرها:
   * اشتباه: عدم درک اینکه نصفِ یا از در عبارت نصف یک دوم به معنای عمل ضرب است.
   * راهکار: تأکید بر اینکه کلمه از در مسائل کسری (مانند کسری از یک عدد یا کسری از یک کسر) معمولاً به معنای عمل ضرب است. تمرین با مثال های ساده تر مانند یک دوم از شش (1/2 × 6) می تواند کمک کننده باشد.
4. مشکل در معکوس کردن کسر در تقسیم:
   * اشتباه: در روش تقسیم، فراموش کردن معکوس کردن کسر دوم یا اشتباه در انجام آن.
   * راهکار: مرور مکرر قاعده تقسیم کسرها (ثابت ماندن کسر اول، تبدیل تقسیم به ضرب، معکوس کردن کسر دوم). استفاده از مثال های متعدد و تمرین های هدفمند برای تثبیت این قاعده.
5. اشتباه در ضرب اعداد اعشاری:
   * اشتباه: در تبدیل به حالت اعشاری (نصف 0.5)، اشتباه در محاسبه 0.5 × 0.5 و نادیده گرفتن جایگاه اعشار.
   * راهکار: مرور دقیق قواعد ضرب اعداد اعشاری، به ویژه شمارش تعداد ارقام اعشاری در عوامل و قرار دادن نقطه اعشار در حاصل ضرب.

با پرداختن به این اشتباهات رایج و ارائه توضیحات روشن و تمرین های کافی، می توان به دانش آموزان کمک کرد تا این مفاهیم را به درستی درک کرده و از بروز خطاهای مشابه در آینده جلوگیری کنند. تکرار، استفاده از روش های بصری و ارتباط دادن مفاهیم به زندگی روزمره، از راهکارهای مؤثر برای غلبه بر این چالش ها هستند.

کاربردهای عملی نصف یک دوم در زندگی روزمره

مفاهیم ریاضیات، حتی آنهایی که در ابتدا انتزاعی به نظر می رسند، اغلب کاربردهای ملموس و عملی در زندگی روزمره ما دارند. درک نصف یک دوم و توانایی انجام محاسبات کسری، در موقعیت های مختلفی به کار می آید:

1. آشپزی و شیرینی پزی:
   * بسیاری از دستورهای غذایی شامل کسرها هستند. مثلاً اگر دستور پخت یک کیک به 1/2 پیمانه آرد نیاز داشته باشد و شما بخواهید نصف آن مقدار کیک را درست کنید، باید نصف 1/2 پیمانه آرد استفاده کنید که می شود 1/4 پیمانه. این کاربرد بسیار رایج و عملی است.
2. خیاطی و طراحی:
   * در خیاطی، ممکن است نیاز باشد ابعاد یک الگو را نصف کنید یا قسمتی از آن را کوچک تر کنید. مثلاً اگر قسمتی از پارچه 1/2 متر باشد و شما بخواهید نصف آن را استفاده کنید، به 1/4 متر پارچه نیاز خواهید داشت.
3. پروژه های DIY (خودت انجام بده) و کار با چوب:
   * در ساخت و سازهای کوچک یا پروژه های خانگی، نیاز به اندازه گیری دقیق و تقسیم بندی مواد است. اگر یک تخته چوب 1/2 اینچ ضخامت داشته باشد و شما بخواهید یک لایه نازک تر که نصف آن است را ایجاد کنید، به 1/4 اینچ ضخامت خواهید رسید.
4. تقسیم مواد و منابع:
   * فرض کنید شما و دوستتان می خواهید یک نوشیدنی 1/2 لیتری را نصف کنید. هر کدام از شما 1/4 لیتر از نوشیدنی را خواهید داشت. این مفهوم در تقسیم هرگونه منبع به کار می رود.
5. درک تخفیف ها و قیمت ها:
   * گاهی اوقات تخفیف ها به صورت کسری بیان می شوند. اگر محصولی با 1/2 قیمت اصلی عرضه شود و سپس تخفیف دیگری اعلام شود که نصف تخفیف قبلی است، برای محاسبه قیمت نهایی باید مفهوم نصف یک دوم را به کار ببرید.
6. ورزش و تمرینات:
   * در برنامه های تمرینی، ممکن است مدت زمان یا شدت یک فعالیت به صورت کسری کاهش یابد. مثلاً اگر قرار باشد 1/2 ساعت بدوید و مربی بگوید امروز نصف آن را بدوید، شما 1/4 ساعت دویده اید.

این مثال ها نشان می دهند که درک و توانایی کار با کسرها و مفاهیم پایه ای مانند نصف یک دوم، تنها به کتاب درسی محدود نمی شود و ابزاری قدرتمند برای حل مسائل روزمره و مدیریت بهتر امور زندگی است. این کاربردها به دانش آموزان انگیزه می دهند تا مفاهیم ریاضی را جدی تر بگیرند و ارتباط آن را با دنیای واقعی درک کنند.

جمع بندی و نتیجه گیری

در این مقاله به بررسی جامع و مفصل مسئله نصف یک دوم چقدر است ریاضی ششم پرداختیم. روشن شد که پاسخ این سوال، با هر رویکردی که پیش بگیریم، «یک چهارم» یا همان 1/4 است. این نتیجه نه تنها از طریق محاسبات دقیق ریاضی (هم با تقسیم کسرها و هم با ضرب کسرها) به دست می آید، بلکه با استفاده از درک بصری و مدل سازی با اشکال نیز تأیید می شود. همچنین، ارتباط این مفهوم با اعداد اعشاری و نحوه محاسبه نصف 0.5 نیز بررسی شد که باز هم به عدد 0.25 (معادل 1/4) ختم می شود.

دانش آموزان با درک هر دو روش تقسیم و ضرب کسرها برای حل این نوع مسائل، می توانند بنیادهای ریاضی خود را تقویت کرده و انعطاف پذیری بیشتری در حل مسائل آتی داشته باشند. این مفهوم، با وجود سادگی، نقش کلیدی در توسعه تفکر کسری، درک نسبت ها و آمادگی برای مفاهیم پیچیده تر ریاضی در مقاطع بالاتر دارد. تسلط بر نصف یک دوم نه تنها یک مهارت آکادمیک است، بلکه ابزاری کاربردی در موقعیت های روزمره، از آشپزی و خیاطی گرفته تا مدیریت منابع و درک تخفیف ها، به شمار می رود.

تشویق دانش آموزان به تمرین بیشتر و حل مسائل مشابه، راهکاری مؤثر برای تثبیت این آموخته ها و کسب اطمینان در به کارگیری صحیح مفاهیم کسری است. یادگیری ریاضی، فراتر از حفظ کردن فرمول ها، نیازمند درک عمیق مفاهیم و توانایی کاربرد آن ها در زمینه های مختلف است.

تمرین برای شما!

برای تقویت درک خود از مفاهیم مطرح شده در این مقاله، سعی کنید مسائل زیر را حل کنید:

1. نصف یک سوم (1/3) چقدر است؟
2. نصف سه چهارم (3/4) چقدر است؟
3. نصف 0.75 چقدر است؟
4. اگر نصف یک کیک، 2/5 کیک باشد، نصف همان قسمت چقدر می شود؟
5. نصف کسر 5/6 چقدر می شود؟

با حل این تمرینات، مهارت شما در کار با کسرها و مفهوم نصف به طور قابل توجهی افزایش خواهد یافت.